周一同学Zelina

Appearance

🎧 序言 ​

在我们的日常生活中，图无处不在。小到一张小小地图，大到我们我们乘坐的航班，每一个都跟图有着紧密的联系。

而对于前端来说，图的应用也是相对比较广泛的。图常用于克隆图、太平洋大西洋水流问题、有效数字的判断等等场景。

在下面的这篇文章中，将讲解关于图的一些基础知识，以及图在前端中的常见应用。

一起来学习吧~☂️

🎤 一、图是什么？ ​

1、定义 ​

  • 图是由顶点的集合和边的集合组成的。
  • 图是网络结构的抽象模型，是一组由边连接的节点。
  • 图可以表示任何二元关系，比如道路、航班……。
  • JS 中没有图，但是可以用 Object 和 Array 构建图。
  • 图的表示法：领接矩阵、邻接表、关联矩阵……

2、举例 ​

地铁线路中每一个站点可以看成是一个顶点，而连接着每个站点的线路可以看做是边。

🎹 二、图的表示法 ​

图通常有两种表示法：领接矩阵和邻接表。下面一起来看这两种表示法~

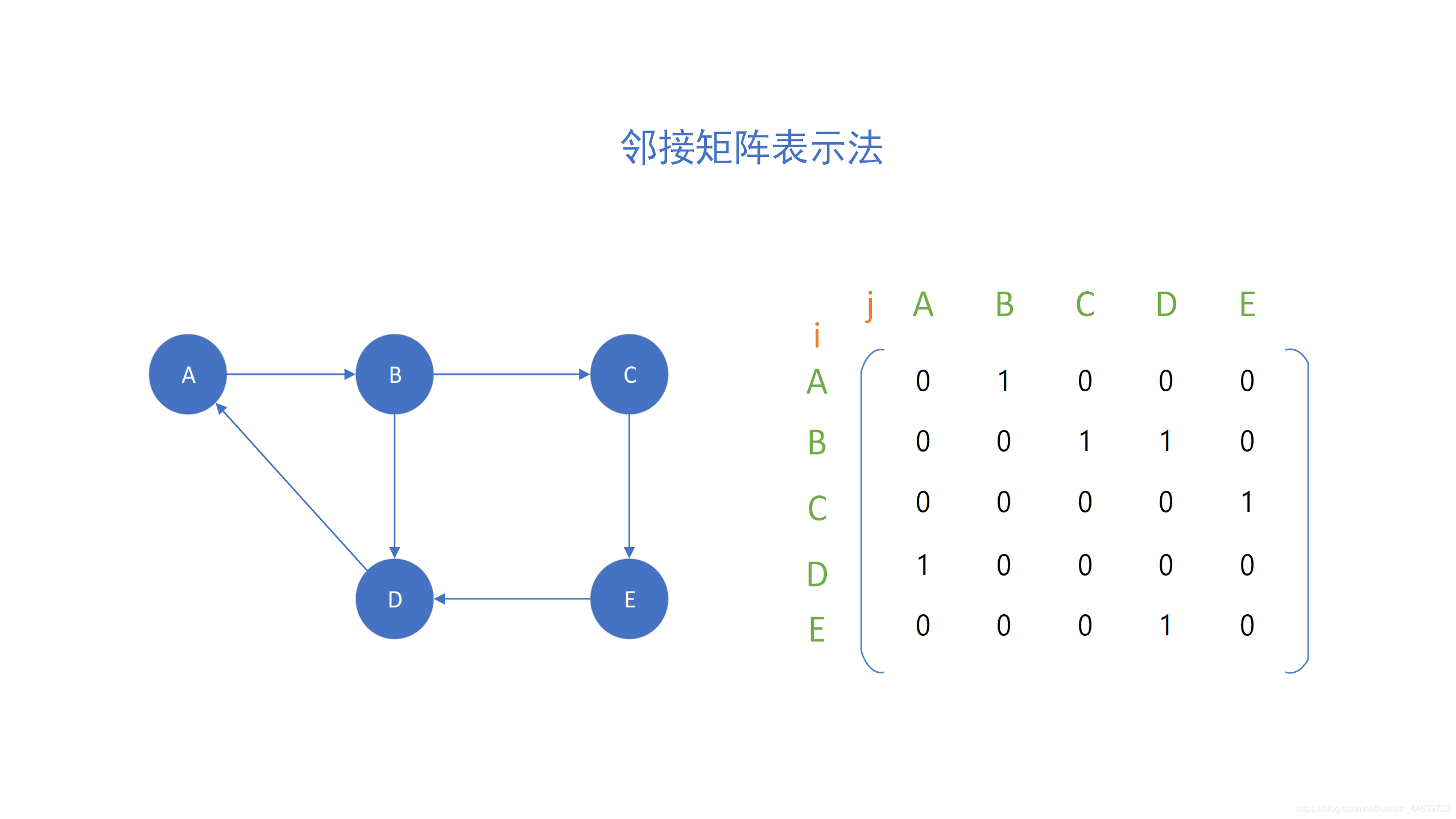
1、邻接矩阵表示法 ​

下面用一张图来展示邻接矩阵的表示法。详情见下图 👇

邻接矩阵表示法

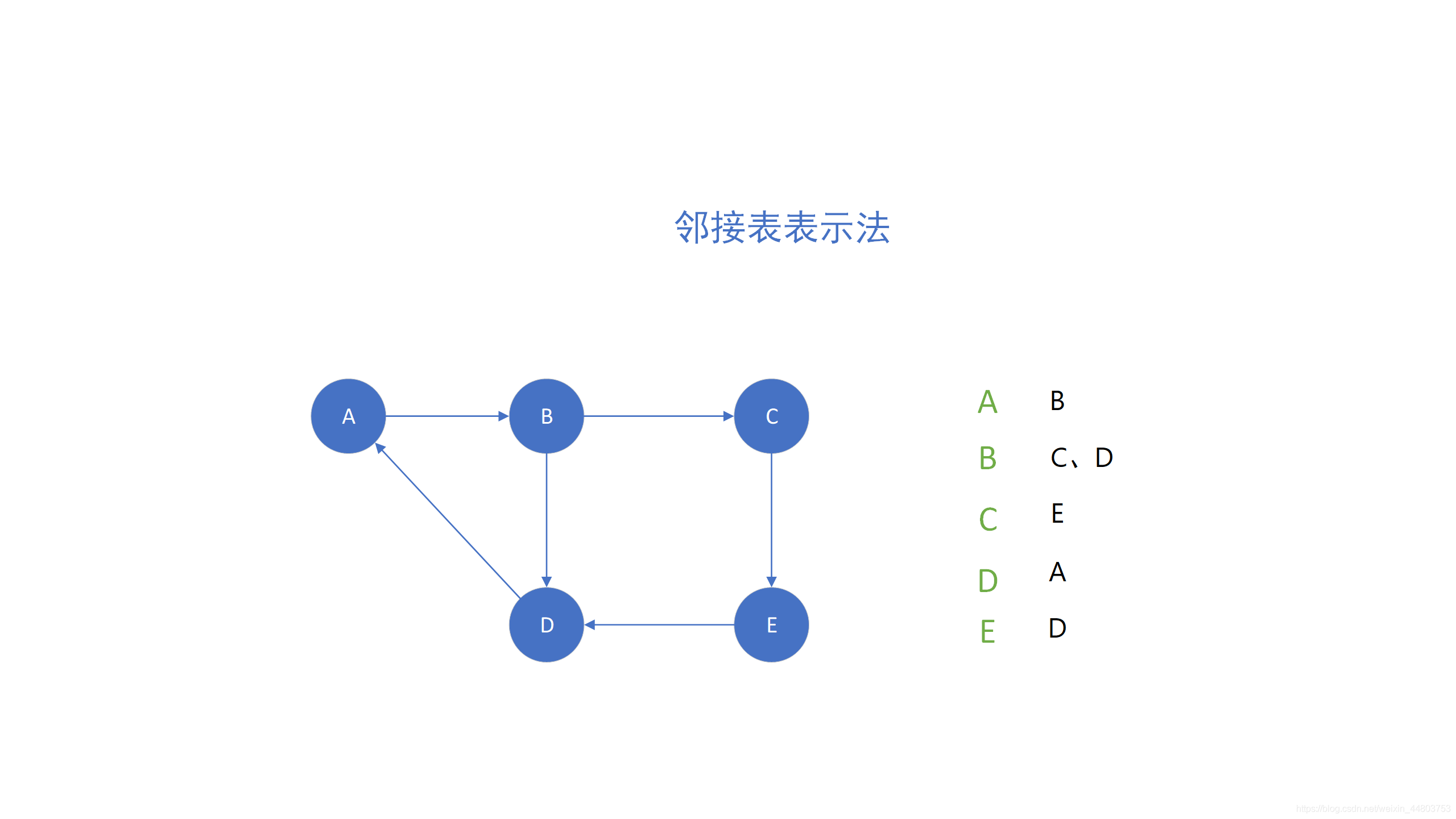
2、邻接表表示法 ​

大家可以看到上面的邻接矩阵，在矩阵中存在着大量的 0，这将会占据程序中大量的内存。因此，我们引入了邻接表，来解决这个问题。详情见下图 👇

邻接表表示法

🎺 三、图的常用操作 ​

1、图的深度优先遍历 ​

（1）定义 ​

  • 图的深度优先遍历，即尽可能深的搜索图的分支。

（2）口诀 ​

  • 访问根节点。
  • 对根节点没访问过的相邻节点挨个进行深度优先遍历。

（3）代码实现 ​

接下来我们用 JS 来实现图的深度优先遍历，这里我们采用邻接表的形式来表示。具体代码如下：

我们先来定义一个图的结构：

js
const graph = {
  0: [1, 2],
  1: [2],
  2: [0, 3],
  3: [3],
};
const graph = {
  0: [1, 2],
  1: [2],
  2: [0, 3],
  3: [3],
};

接下来来对这个结构进行深度优先遍历：

js
const visited = new Set();

const dfs = (n) => {
  console.log(n);
  //将访问过的节点加入集合中
  visited.add(n);
  //对当前节点所对应的数组挨个进行遍历
  graph[n].forEach((c) => {
    // 对没有访问过的在此访问
    if (!visited.has(c)) {
      //递归进行深度遍历
      dfs(c);
    }
  });
};
//以2为起始点进行深度优先遍历
dfs(2);
const visited = new Set();

const dfs = (n) => {
  console.log(n);
  //将访问过的节点加入集合中
  visited.add(n);
  //对当前节点所对应的数组挨个进行遍历
  graph[n].forEach((c) => {
    // 对没有访问过的在此访问
    if (!visited.has(c)) {
      //递归进行深度遍历
      dfs(c);
    }
  });
};
//以2为起始点进行深度优先遍历
dfs(2);

最后我们来看下打印结果：

js
/*打印结果：
2
0
1
3
*/
/*打印结果：
2
0
1
3
*/

2、图的广度优先遍历 ​

（1）定义 ​

  • 图的广度优先遍历，先访问离根节点最近的节点。

（2）口诀 ​

  • 新建一个队列，把根节点入队。
  • 把队头出队并访问。
  • 把队头每访问过的相邻节点入队。
  • 重复第二、三步操作，直到队列为空。

（3）代码实现 ​

接下来我们用 JS 来实现图的广度优先遍历，这里我们采用邻接表的形式来表示。具体代码如下：

同样地我们先来定义一个图的结构：

js
const graph = {
  0: [1, 2],
  1: [2],
  2: [0, 3],
  3: [3],
};
const graph = {
  0: [1, 2],
  1: [2],
  2: [0, 3],
  3: [3],
};

接下来来对这个结构进行深度优先遍历：

js
//新建一个集合，存放访问过的节点
const visited = new Set();
//初始节点放进集合中
visited.add(2);
//将初始节点放入队列q中
const q = [2];

while (q.length) {
  //删除队列q的第一个元素，并将其值返回
  const n = q.shift();
  //打印返回后的值
  console.log(n);
  //将该值所对应邻接表的数组，挨个进行遍历
  graph[n].forEach((c) => {
    //判断数组中的元素是否已经访问过
    if (!visited.has(c)) {
      //如果没有访问过则加入访问队列和访问集合
      q.push(c);
      visited.add(c);
    }
  });
}
//新建一个集合，存放访问过的节点
const visited = new Set();
//初始节点放进集合中
visited.add(2);
//将初始节点放入队列q中
const q = [2];

while (q.length) {
  //删除队列q的第一个元素，并将其值返回
  const n = q.shift();
  //打印返回后的值
  console.log(n);
  //将该值所对应邻接表的数组，挨个进行遍历
  graph[n].forEach((c) => {
    //判断数组中的元素是否已经访问过
    if (!visited.has(c)) {
      //如果没有访问过则加入访问队列和访问集合
      q.push(c);
      visited.add(c);
    }
  });
}

最后我们来看下打印结果：

js
/*打印结果：
2
0
3
1
*/
/*打印结果：
2
0
3
1
*/

🎻 四、leetcode 经典题目解析 ​

接下来我们引用几道经典的 leetcode 算法，来巩固图的知识。

温馨小提示： 题意的内容范例是对官方题目的简单概要，并不是特别全面，建议大家先点击链接查看，使用体验更为友好~

1、leetcode417 太平洋大西洋水流问题（中等） ​

（1）题意

附上题目链接：leetcode417 太平洋大西洋水流问题

给定一个 m x n 的非负整数矩阵来表示一片大陆上各个单元格的高度。“太平洋”处于大陆的左边界和上边界，而“大西洋”处于大陆的右边界和下边界。

规定水流只能按照上、下、左、右四个方向流动，且只能从高到低或者在同等高度上流动。

请找出那些水流既可以流动到“太平洋”，又能流动到“大西洋”的陆地单元的坐标。

提示：

  • 输出坐标的顺序不重要

  • m 和 n 都小于 150

    输入输出示例：

  • bash
    给定下面的 5x5 矩阵:

  太平洋 ~   ~   ~   ~   ~
       ~  1   2   2   3  (5) *
       ~  3   2   3  (4) (4) *
       ~  2   4  (5)  3   1  *
       ~ (6) (7)  1   4   5  *
       ~ (5)  1   1   2   4  *
          *   *   *   *   * 大西洋

返回:

[[0, 4], [1, 3], [1, 4], [2, 2], [3, 0], [3, 1], [4, 0]] (上图中带括号的单元).
    给定下面的 5x5 矩阵:

  太平洋 ~   ~   ~   ~   ~
       ~  1   2   2   3  (5) *
       ~  3   2   3  (4) (4) *
       ~  2   4  (5)  3   1  *
       ~ (6) (7)  1   4   5  *
       ~ (5)  1   1   2   4  *
          *   *   *   *   * 大西洋

返回:

[[0, 4], [1, 3], [1, 4], [2, 2], [3, 0], [3, 1], [4, 0]] (上图中带括号的单元).

（2）解题思路

  • 把矩阵想象成图。
  • 从海岸线逆流而上遍历图，所到之处就是可以留到某个大洋的坐标。

（3）解题步骤

  • 新建两个矩阵，分别记录能留到两个大洋的坐标。
  • 从海岸线，多管旗下，同时深度优先遍历图，过程中填充上述矩阵。
  • 遍历两个矩阵，找出能流到两个大洋的坐标。

（4）代码实现

js
/**
 * @param {number[][]} matrix
 * @return {number[][]}
 */
let pacificAtlantic = function (matrix) {
  // 如果传入的不是一个矩阵，则返回一个空数组
  if (!matrix && !matrix[0]) {
    return [];
  }
  // m表示矩阵的行数，n表示矩阵的列数
  const m = matrix.length;
  // matrix[0]表示矩阵的第一行
  const n = matrix[0].length;
  // 定义flow1记录留到太平洋的坐标，flow2记录留到大西洋的坐标
  // from方法构建长度为m的数组,第二个参数填充指定数组的值填充为什么样
  const flow1 = Array.from({ length: m }, () => new Array(n).fill(false));
  const flow2 = Array.from({ length: m }, () => new Array(n).fill(false));
  // console.log(flow1);
  // console.log(flow2);

  // 进行深度优先遍历
  // r即row,表示行；c即column，表示列
  // flow为二维数组
  const dfs = (r, c, flow) => {
    flow[r][c] = true;
    [
      [r - 1, c],
      [r + 1, c],
      [r, c - 1],
      [r, c + 1],
    ].forEach(([nr, nc]) => {
      if (
        // 保证在矩阵中
        nr >= 0 &&
        nr < m &&
        nc >= 0 &&
        nc < n &&
        // 防止死循环
        !flow[nr][nc] &&
        // 保证逆流而上，即保证下一个节点的值大于上一个节点的值
        matrix[nr][nc] >= matrix[r][c]
      ) {
        dfs(nr, nc, flow);
      }
    });
  };

  // 沿着海岸线逆流而上
  for (let r = 0; r < m; r++) {
    //第一列的流到太平洋，即flow1
    dfs(r, 0, flow1);
    //最后一列的留到大西洋，即flow2
    dfs(r, n - 1, flow2);
  }

  for (let c = 0; c < n; c++) {
    //第一行的流到太平洋，即flow1
    dfs(0, c, flow1);
    //最后一行的留到大西洋，即flow2
    dfs(m - 1, c, flow2);
  }

  //收集能留到两个大洋里的坐标
  const res = [];
  for (let r = 0; r < m; r++) {
    for (let c = 0; c < n; c++) {
      //当flow1和flow2都为true时，则说明既能留到太平洋，也能流到大西洋
      if (flow1[r][c] && flow2[r][c]) {
        res.push([r, c]);
      }
    }
  }
  return res;
};
console.log(
  pacificAtlantic([
    [1, 2, 2, 3, 5],
    [3, 2, 3, 4, 4],
    [2, 4, 5, 3, 1],
    [6, 7, 1, 4, 5],
    [5, 1, 1, 2, 4],
  ])
);

/*打印结果：
[
  [ 0, 4 ], [ 1, 3 ],
  [ 1, 4 ], [ 2, 2 ],
  [ 3, 0 ], [ 3, 1 ],
  [ 4, 0 ]
]
*/
/**
 * @param {number[][]} matrix
 * @return {number[][]}
 */
let pacificAtlantic = function (matrix) {
  // 如果传入的不是一个矩阵，则返回一个空数组
  if (!matrix && !matrix[0]) {
    return [];
  }
  // m表示矩阵的行数，n表示矩阵的列数
  const m = matrix.length;
  // matrix[0]表示矩阵的第一行
  const n = matrix[0].length;
  // 定义flow1记录留到太平洋的坐标，flow2记录留到大西洋的坐标
  // from方法构建长度为m的数组,第二个参数填充指定数组的值填充为什么样
  const flow1 = Array.from({ length: m }, () => new Array(n).fill(false));
  const flow2 = Array.from({ length: m }, () => new Array(n).fill(false));
  // console.log(flow1);
  // console.log(flow2);

  // 进行深度优先遍历
  // r即row,表示行；c即column，表示列
  // flow为二维数组
  const dfs = (r, c, flow) => {
    flow[r][c] = true;
    [
      [r - 1, c],
      [r + 1, c],
      [r, c - 1],
      [r, c + 1],
    ].forEach(([nr, nc]) => {
      if (
        // 保证在矩阵中
        nr >= 0 &&
        nr < m &&
        nc >= 0 &&
        nc < n &&
        // 防止死循环
        !flow[nr][nc] &&
        // 保证逆流而上，即保证下一个节点的值大于上一个节点的值
        matrix[nr][nc] >= matrix[r][c]
      ) {
        dfs(nr, nc, flow);
      }
    });
  };

  // 沿着海岸线逆流而上
  for (let r = 0; r < m; r++) {
    //第一列的流到太平洋，即flow1
    dfs(r, 0, flow1);
    //最后一列的留到大西洋，即flow2
    dfs(r, n - 1, flow2);
  }

  for (let c = 0; c < n; c++) {
    //第一行的流到太平洋，即flow1
    dfs(0, c, flow1);
    //最后一行的留到大西洋，即flow2
    dfs(m - 1, c, flow2);
  }

  //收集能留到两个大洋里的坐标
  const res = [];
  for (let r = 0; r < m; r++) {
    for (let c = 0; c < n; c++) {
      //当flow1和flow2都为true时，则说明既能留到太平洋，也能流到大西洋
      if (flow1[r][c] && flow2[r][c]) {
        res.push([r, c]);
      }
    }
  }
  return res;
};
console.log(
  pacificAtlantic([
    [1, 2, 2, 3, 5],
    [3, 2, 3, 4, 4],
    [2, 4, 5, 3, 1],
    [6, 7, 1, 4, 5],
    [5, 1, 1, 2, 4],
  ])
);

/*打印结果：
[
  [ 0, 4 ], [ 1, 3 ],
  [ 1, 4 ], [ 2, 2 ],
  [ 3, 0 ], [ 3, 1 ],
  [ 4, 0 ]
]
*/

2、leetcode133 克隆图（中等） ​

（1）题意

附上题目链接：leetcode133 克隆图

给你无向 连通 图中一个节点的引用，请你返回该图的 深拷贝（克隆）。

图中的每个节点都包含它的值 val（int） 和其邻居的列表（list[Node]）。

js
class Node {
    public int val;
    public List<Node> neighbors;
}
class Node {
    public int val;
    public List<Node> neighbors;
}

输入输出示例：

  • 输入: adjList = [[2,4],[1,3],[2,4],[1,3]]
  • 输出: [[2,4],[1,3],[2,4],[1,3]]
  • 解释：
    • 图中有 4 个节点。
    • 节点 1 的值是 1，它有两个邻居：节点 2 和 4 。
    • 节点 2 的值是 2，它有两个邻居：节点 1 和 3 。
    • 节点 3 的值是 3，它有两个邻居：节点 2 和 4 。
    • 节点 4 的值是 4，它有两个邻居：节点 1 和 3 。

（2）解题思路

  • 拷贝所有节点。
  • 拷贝所有的边。

（3）解题步骤

  • 深度或广度优先遍历所有节点。
  • 拷贝所有的结点，存储起来。
  • 将拷贝的结点，按照原图的连接方法进行连接。

（4）代码实现

我们用两种方式来实现克隆图：深度优先遍历和广度优先遍历。具体代码如下：

深度优先遍历：

js
/**
 * // Definition for a Node.
 * function Node(val, neighbors) {
 *    this.val = val === undefined ? 0 : val;
 *    //邻居节点是一个数组
 *    this.neighbors = neighbors === undefined ? [] : neighbors;
 * };
 */

/**
 * @param {Node} node
 * @return {Node}
 */
// 深度优先遍历
let cloneGraph1 = function (node) {
  //如果当前节点为空，则直接返回
  if (!node) {
    return;
  }

  //定义一个字典，存放访问过的节点
  const visited = new Map();
  //深度优先遍历
  const dfs = (n) => {
    // 拷贝一份当前初始节点的值
    const nCopy = new Node(n.val);
    //将拷贝后的节点放到访问字典当中
    visited.set(n, nCopy);
    //对初始节点的邻居节点挨个进行遍历
    (n.neighbors || []).forEach((ne) => {
      //判断访问队列是否有过邻居节点
      if (!visited.has(ne)) {
        /* 如果访问队列没有过该邻居节点，
                则将邻居节点继续进行深度遍历*/
        dfs(ne);
      }
      // 将访问过的邻居节点的值拷贝到nCopy上
      nCopy.neighbors.push(visited.get(ne));
    });
  };
  dfs(node);
  return visited.get(node);
};
/**
 * // Definition for a Node.
 * function Node(val, neighbors) {
 *    this.val = val === undefined ? 0 : val;
 *    //邻居节点是一个数组
 *    this.neighbors = neighbors === undefined ? [] : neighbors;
 * };
 */

/**
 * @param {Node} node
 * @return {Node}
 */
// 深度优先遍历
let cloneGraph1 = function (node) {
  //如果当前节点为空，则直接返回
  if (!node) {
    return;
  }

  //定义一个字典，存放访问过的节点
  const visited = new Map();
  //深度优先遍历
  const dfs = (n) => {
    // 拷贝一份当前初始节点的值
    const nCopy = new Node(n.val);
    //将拷贝后的节点放到访问字典当中
    visited.set(n, nCopy);
    //对初始节点的邻居节点挨个进行遍历
    (n.neighbors || []).forEach((ne) => {
      //判断访问队列是否有过邻居节点
      if (!visited.has(ne)) {
        /* 如果访问队列没有过该邻居节点，
                则将邻居节点继续进行深度遍历*/
        dfs(ne);
      }
      // 将访问过的邻居节点的值拷贝到nCopy上
      nCopy.neighbors.push(visited.get(ne));
    });
  };
  dfs(node);
  return visited.get(node);
};

广度优先遍历：

js
/**
 * // Definition for a Node.
 * function Node(val, neighbors) {
 *    this.val = val === undefined ? 0 : val;
 *    //邻居节点是一个数组
 *    this.neighbors = neighbors === undefined ? [] : neighbors;
 * };
 */

/**
 * @param {Node} node
 * @return {Node}
 */
let cloneGraph2 = function (node) {
  //如果当前节点为空，则直接返回
  if (!node) {
    return;
  }
  //定义一个字典，存放访问过的节点
  const visited = new Map();
  //visited存放节点以及节点的值
  visited.set(node, new Node(node.val));
  // 初始化一个队列
  const q = [node];
  // 当队列内有节点信息时
  while (q.length) {
    // 删除队列中的第一个元素并返回值
    const n = q.shift();
    //将节点的邻居挨个进行遍历
    (n.neighbors || []).forEach((ne) => {
      // 判断访问队列是否有过邻居节点
      if (!visited.has(ne)) {
        // 将节点的邻居加入到队列中
        q.push(ne);
        // 将节点的邻居及邻居的值放入visited中
        visited.set(ne, new Node(ne.val));
      }
      /*如果访问队列已经有过该节点，
            则将此节点放入访问队列的邻居节点
             */
      visited.get(n).neighbors.push(visited.get(ne));
    });
  }
  //返回访问队列的节点信息
  return visited.get(node);
};
/**
 * // Definition for a Node.
 * function Node(val, neighbors) {
 *    this.val = val === undefined ? 0 : val;
 *    //邻居节点是一个数组
 *    this.neighbors = neighbors === undefined ? [] : neighbors;
 * };
 */

/**
 * @param {Node} node
 * @return {Node}
 */
let cloneGraph2 = function (node) {
  //如果当前节点为空，则直接返回
  if (!node) {
    return;
  }
  //定义一个字典，存放访问过的节点
  const visited = new Map();
  //visited存放节点以及节点的值
  visited.set(node, new Node(node.val));
  // 初始化一个队列
  const q = [node];
  // 当队列内有节点信息时
  while (q.length) {
    // 删除队列中的第一个元素并返回值
    const n = q.shift();
    //将节点的邻居挨个进行遍历
    (n.neighbors || []).forEach((ne) => {
      // 判断访问队列是否有过邻居节点
      if (!visited.has(ne)) {
        // 将节点的邻居加入到队列中
        q.push(ne);
        // 将节点的邻居及邻居的值放入visited中
        visited.set(ne, new Node(ne.val));
      }
      /*如果访问队列已经有过该节点，
            则将此节点放入访问队列的邻居节点
             */
      visited.get(n).neighbors.push(visited.get(ne));
    });
  }
  //返回访问队列的节点信息
  return visited.get(node);
};

3、leetcode65 有效数字（困难） ​

（1）题意

附上题目链接：leetcode65 有效数字

有效数字（按顺序）可以分成以下几个部分：

  • 一个 小数 或者 整数
  • （可选）一个 'e' 或 'E' ，后面跟着一个 整数

小数（按顺序）可以分成以下几个部分：

  • （可选）一个符号字符（'+' 或 '-'）

  • 下述格式之一：

    • 至少一位数字，后面跟着一个点 '.'
    • 至少一位数字，后面跟着一个点 '.' ，后面再跟着至少一位数字
    • 一个点 '.' ，后面跟着至少一位数字

整数（按顺序）可以分成以下几个部分：

  • （可选）一个符号字符（'+' 或 '-'）

  • 至少一位数字

    输入输出示例：

  • 输入: s = "0"

  • 输出: true

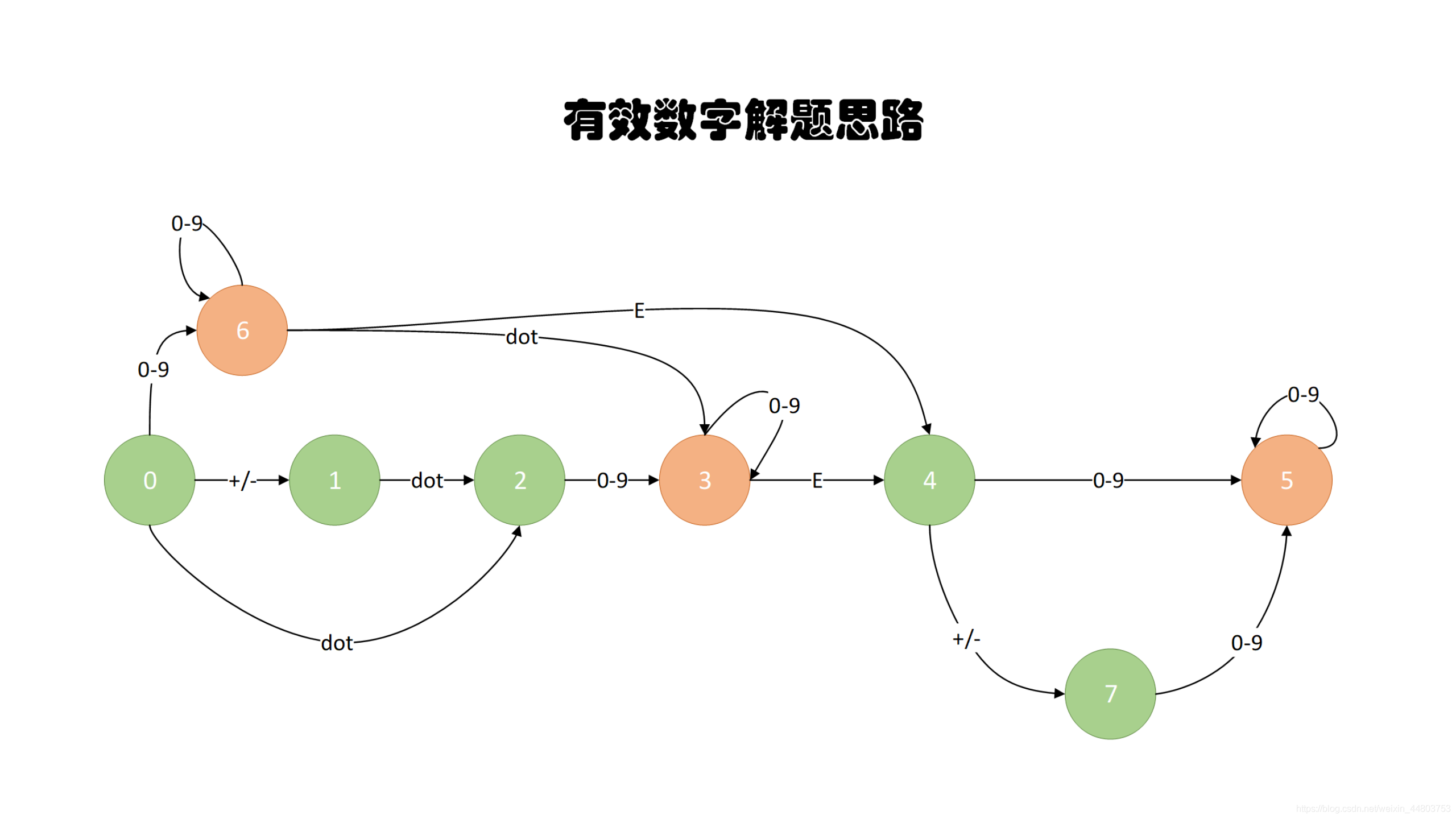
（2）解题思路-图例

有效数字图例

（3）解题步骤

  • 构建一个表示状态的图。
  • 遍历字符串，并沿着图走，如果到了某个节点无路可走就返回 false。
  • 遍历结束，如走到 3/5/6，就返回 true，否则返回 false。

（4）代码实现

js
let isNumber = function (s) {
  const graph = {
    0: { blank: 0, sign: 1, '.': 2, digit: 6 },
    1: { digit: 6, '.': 2 },
    2: { digit: 3 },
    3: { digit: 3, e: 4 },
    4: { digit: 5, sign: 7 },
    5: { digit: 5 },
    6: { digit: 6, '.': 3, e: 4 },
    7: { digit: 5 },
  };

  let state = 0;
  for (c of s.trim()) {
    if (c >= '0' && c <= '9') {
      c = 'digit';
    } else if (c === ' ') {
      c = 'blank';
    } else if (c === '+' || c === '-') {
      c = 'sign';
    }
    state = graph[state][c];
    if (state === undefined) {
      return false;
    }
  }
  if (state === 3 || state === 5 || state === 6) {
    return true;
  }
  return false;
};
let isNumber = function (s) {
  const graph = {
    0: { blank: 0, sign: 1, '.': 2, digit: 6 },
    1: { digit: 6, '.': 2 },
    2: { digit: 3 },
    3: { digit: 3, e: 4 },
    4: { digit: 5, sign: 7 },
    5: { digit: 5 },
    6: { digit: 6, '.': 3, e: 4 },
    7: { digit: 5 },
  };

  let state = 0;
  for (c of s.trim()) {
    if (c >= '0' && c <= '9') {
      c = 'digit';
    } else if (c === ' ') {
      c = 'blank';
    } else if (c === '+' || c === '-') {
      c = 'sign';
    }
    state = graph[state][c];
    if (state === undefined) {
      return false;
    }
  }
  if (state === 3 || state === 5 || state === 6) {
    return true;
  }
  return false;
};

🎸 五、结束语 ​

通过上文的学习，我们了解到了图的两种表示法：邻接矩阵表示法和邻接表表示法。同时，还学习了图的两种常用操作：图的深度优先遍历和图的广度优先遍历。最后，我们引用了几道 leetcode 算法题，来解决了图的一些常用场景。

个人认为，图相对于其他数据结构来说，学习难度更大一点，但又是一个不得不学的基本知识，所以还是得多加练习。

除此之外呢，对于以上算法题，学有余力之余，可以考虑多调试，一步步跟着调试走，慢慢的就理解的更透彻了。

关于图在前端中的应用讲到这里就结束啦！希望对大家有帮助~

🐣 彩蛋时间 Painted Eggshell ​

往期推荐 ​

栈 👉栈在前端中的应用，顺便再了解下深拷贝和浅拷贝！

队列 👉详解队列在前端的应用，深剖 JS 中的事件循环 Eventloop，再了解微任务和宏任务

链表 👉详解链表在前端的应用，顺便再弄懂原型和原型链！

字典和集合 👉ES6 的 Set 和 Map 你都知道吗？一文了解集合和字典在前端中的应用

树 👉一文了解树在前端中的应用，掌握数据结构中树的生命线

动态规则和分而治之算法 👉一文了解分而治之和动态规则算法在前端中的应用

贪心算法和回溯算法 👉一文了解贪心算法和回溯算法在前端中的应用

Released under the MIT License.

Copyright © 2021-present 周一