📻 前言
平常在日常生活中,我们总会遇到公平性这个话题。比如,几个人分奖品,怎么样才能公平分配?又或者,年会来个抽奖转盘,怎么样才能让它更公平呢?
那在下面这篇文章呢,我们将谈论关于洗牌的公平性。一起来了解吧~
一、🎙️ 需求分析 - 洗牌问题
有时候我们在闲暇之余可能会打打斗地主之类的扑克游戏,但是这扑克要怎么去洗牌,才能不失公平性呢?

那么接下来,我们由浅入深的来讲解一种实现效果。
二、💿 实现版本
1. 版本一:常规思维
先附上代码:
JS 代码:
const cards = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9];
function shuffle(cards) {
return [...cards].sort(() => (Math.random() > 0.5 ? -1 : 1));
}
console.log(shuffle(cards)); // [5, 4, 3, 2, 1, 9, 0, 6, 8, 7]const cards = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9];
function shuffle(cards) {
return [...cards].sort(() => (Math.random() > 0.5 ? -1 : 1));
}
console.log(shuffle(cards)); // [5, 4, 3, 2, 1, 9, 0, 6, 8, 7]如果说要公平,那很多小伙伴刚开始想的应该是随机打乱。但是其实 Math.random() 并不能真正起到真正的随机。
它的随机性跟原来的位置相关,它是随机的去交换原来两个数的位置,而这个位置是否会产生交换的不确定性也很大,所以它并没办法达到真正的公平。
2. 版本二:验证公平性
先附上代码:
JS 代码:
const cards = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9];
function shuffle(cards) {
return [...cards].sort(() => (Math.random() > 0.5 ? -1 : 1));
}
const result = Array(10).fill(0);
for (let i = 0; i < 1000000; i++) {
const c = shuffle(cards);
for (let j = 0; j < 10; j++) {
result[j] += c[j];
}
}
console.log(result);const cards = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9];
function shuffle(cards) {
return [...cards].sort(() => (Math.random() > 0.5 ? -1 : 1));
}
const result = Array(10).fill(0);
for (let i = 0; i < 1000000; i++) {
const c = shuffle(cards);
for (let j = 0; j < 10; j++) {
result[j] += c[j];
}
}
console.log(result);依据版本一的例子,我们来看下它为什么不公平。先看下打印效果:
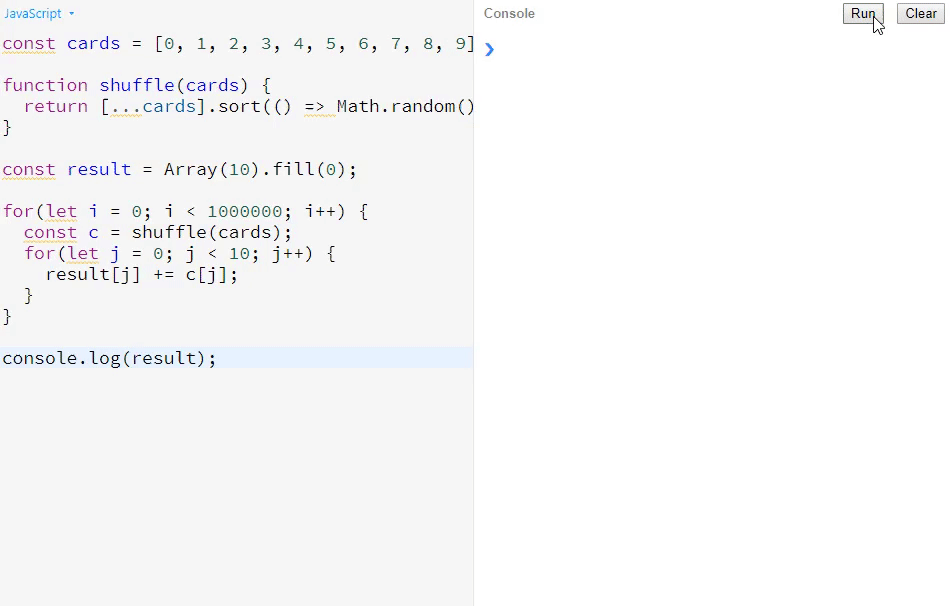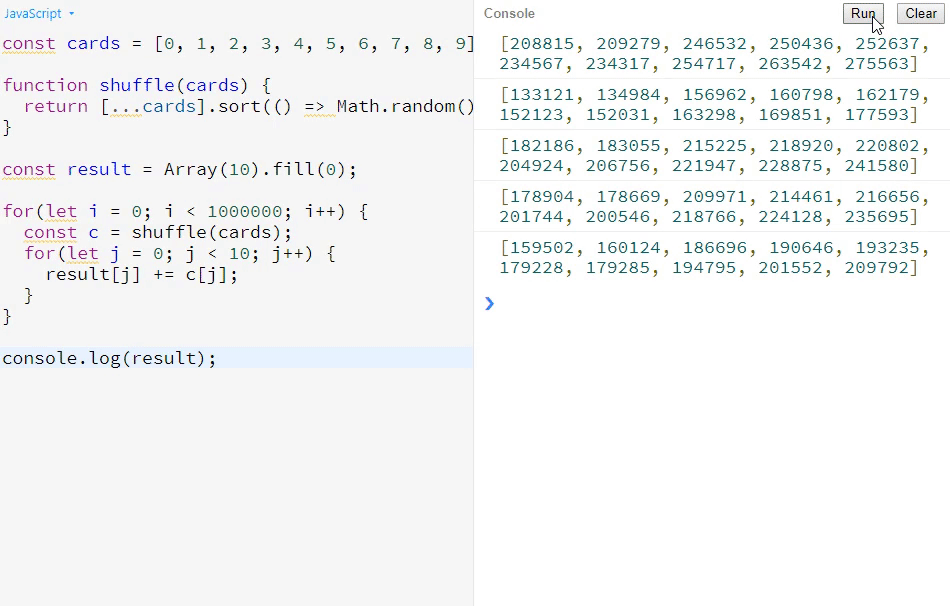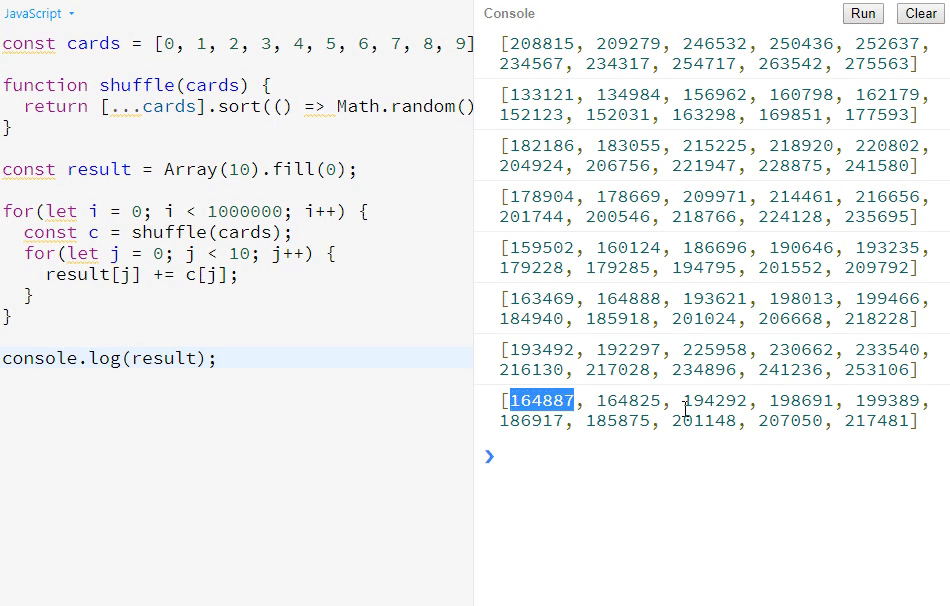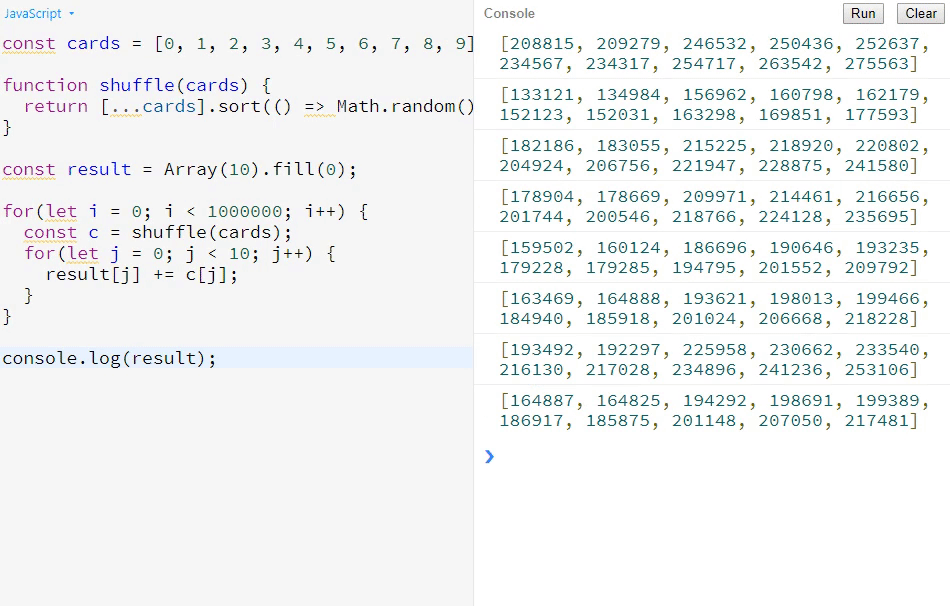
大家可以看到,如果这个算法是公平的,那它从第一个数到最后一个数应该都是比较平均的,而在这个算法中,越靠后的数,其数值会越大,所以这个随机性明显是有问题的。一般来说,如果用这个算法的话,排在越后面的同学的中奖概率,会比排在前面的同学的中奖概率要小。
3. 版本三:交换法则
先附上代码:
JS 代码:
const cards = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9];
function shuffle(cards) {
const c = [...cards];
for (let i = c.length; i > 0; i--) {
const pIdx = Math.floor(Math.random() * i);
[c[pIdx], c[i - 1]] = [c[i - 1], c[pIdx]];
}
return c;
}
//验证是否公平
const result = Array(10).fill(0);
for (let i = 0; i < 10000; i++) {
const c = shuffle(cards);
for (let j = 0; j < 10; j++) {
result[j] += c[j];
}
}
console.log(shuffle(cards));
console.log(result);const cards = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9];
function shuffle(cards) {
const c = [...cards];
for (let i = c.length; i > 0; i--) {
const pIdx = Math.floor(Math.random() * i);
[c[pIdx], c[i - 1]] = [c[i - 1], c[pIdx]];
}
return c;
}
//验证是否公平
const result = Array(10).fill(0);
for (let i = 0; i < 10000; i++) {
const c = shuffle(cards);
for (let j = 0; j < 10; j++) {
result[j] += c[j];
}
}
console.log(shuffle(cards));
console.log(result);基于前面两个版本的瑕疵,我们来实现一种公平的写法。上面的这种算法呢,其复杂度是 O(n) ,它的实现逻辑是,在整个有序数组中,先随机抽取任意一个数,把它放到最后的位置,之后再随机抽取任意一个数,再把它换到最后一个位置进行交换,以此类推。具体思路如下图所示:

下面来看控制台打印效果:
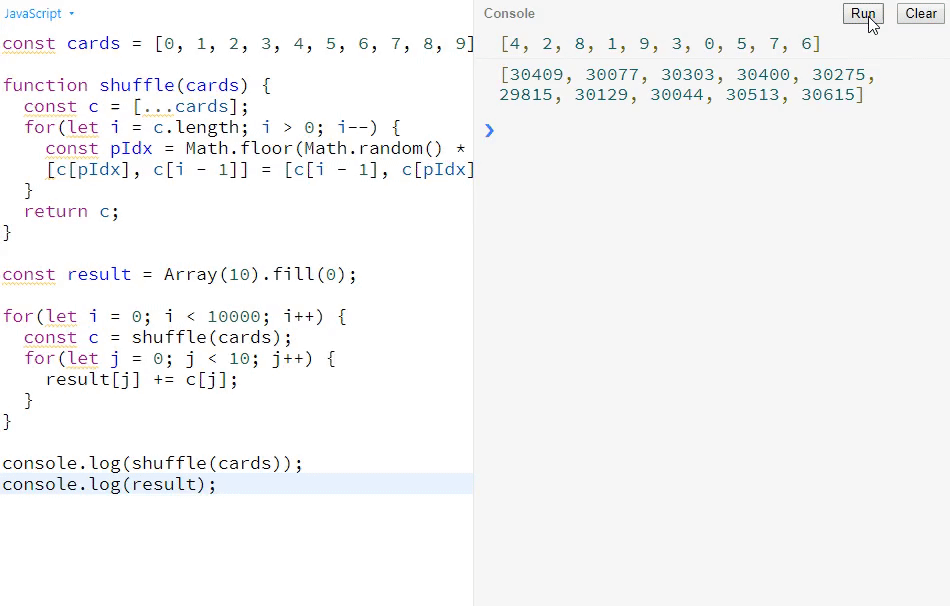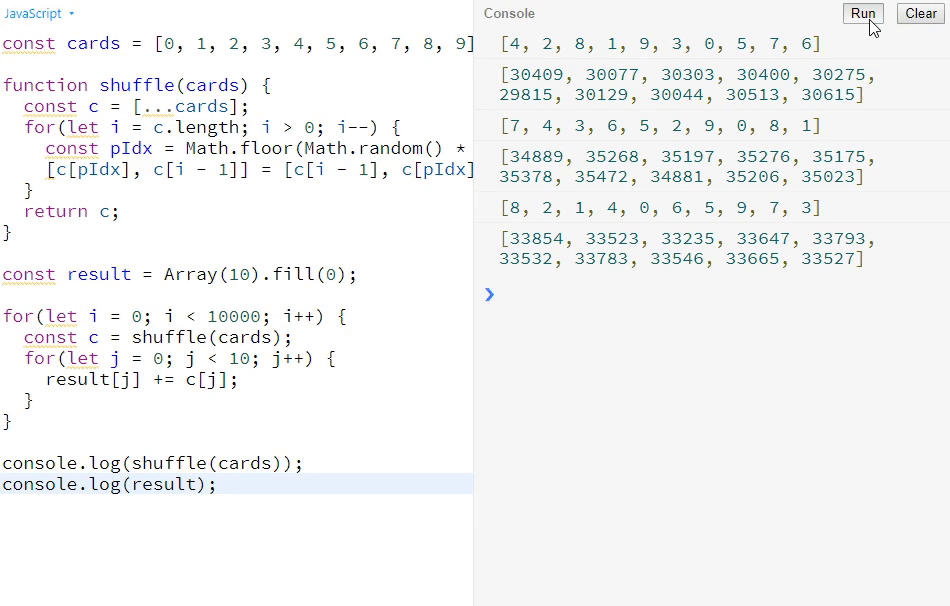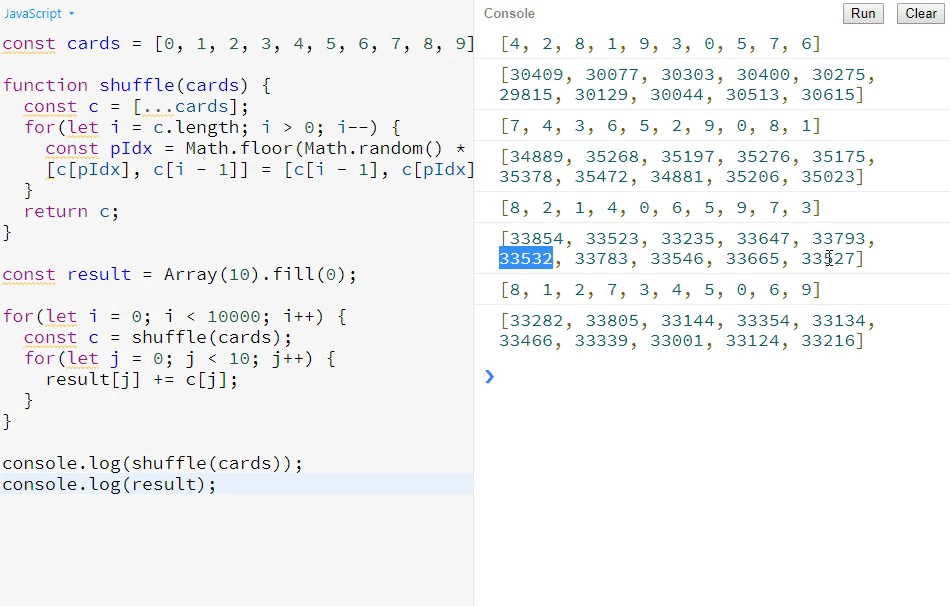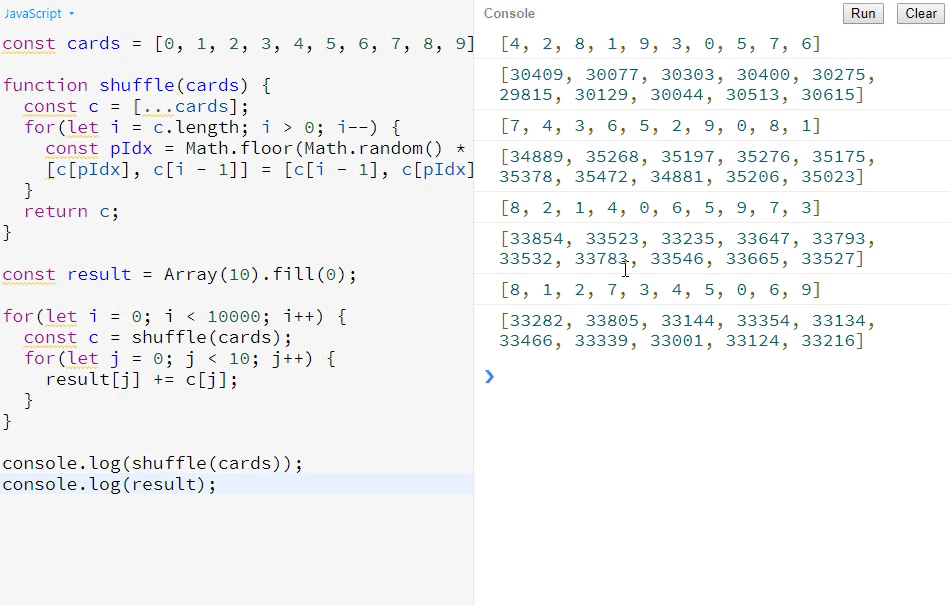
大家可以看到,控制台打印出来的数都是相对比较平均的,而不会前后差异特别大。所以,这个算法是公平的。
三、📺 在线 Online
以上三个版本的在线地址:
四、📹 结束语
在上面的文章中,我们首先谈论了平常常用的随机洗牌法的不公平性,之后重新介绍了一种新的交换法则来实现洗牌的公平性。不知道大家对洗牌问题是否有了进一步了解呢?
如果您觉得这篇文章有帮助到您的的话不妨点赞支持一下哟~~😉